一种针对Saber密钥封装机制的侧信道攻击
背景介绍
CHES 2022上,来自南京农业大学李延斌教授的团队提出了第一种针对Toom-Cook算法的基于软分析侧信道攻击(SASCA)的单能量迹攻击方法[1],并通过优化因子图、改进置信度传播(BP)等方式优化攻击流程,大大增强了攻击的实用性。
Toom-Cook是一种经典的基于分治思想的多项式乘法算法。自NIST(美国国家标准与技术研究院)的后量子标准化程序开始以来,基于Toom-Cook的多项式乘法算法重新受到关注。作者以基于Toom-Cook乘法实现的密钥封装机制Saber为实例,研究后量子密码在嵌入式密码设备上的实现安全性。
相关知识
1、Saber中的多项式乘法
在Saber中,密文和密钥都是255阶的多项式,为了方便快捷地求取它们的乘积,采用Toom-Cook-4和二阶Karatsuba算法将256*256的多项式乘法转变为16*16的多项式乘法。
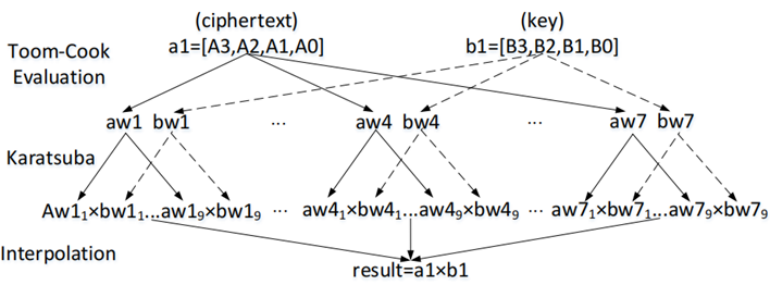
图1 Saber中的多项式乘法
2、SASCA
SASCA是2014年提出的一种侧信道攻击方法,它将泄露的侧信息以类LDPC编码的形式表示。其攻击方法可以简单描述为构建因子图模型,计算泄露的中间变量的后验分布概率,然后在算法的整个计算过程中互相传播分布信息,最终计算得到密钥的边缘分布的过程。SASCA结合了模板匹配和BP算法,能够有效地利用攻击中的任何泄露。
攻击及优化方法
1、攻击方法
对应Saber中的Schoolbook、Karatsuba和Toom-Cook三种乘法,作者分别构建SFG、KFG和TFG三类因子图。
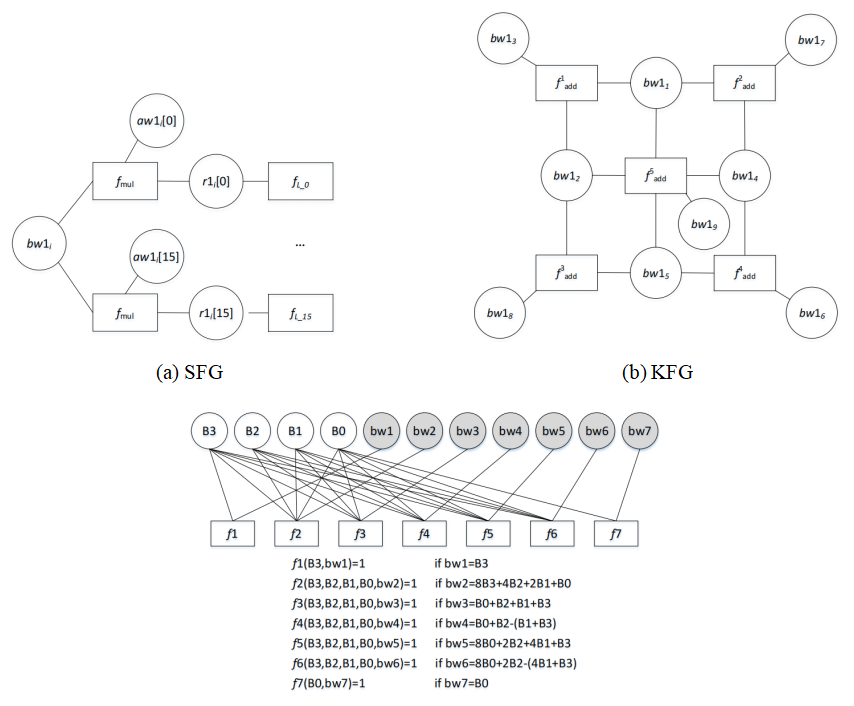
图2 三类因子图
这三类因子图构成了Saber中的多项式乘法的完整因子图。
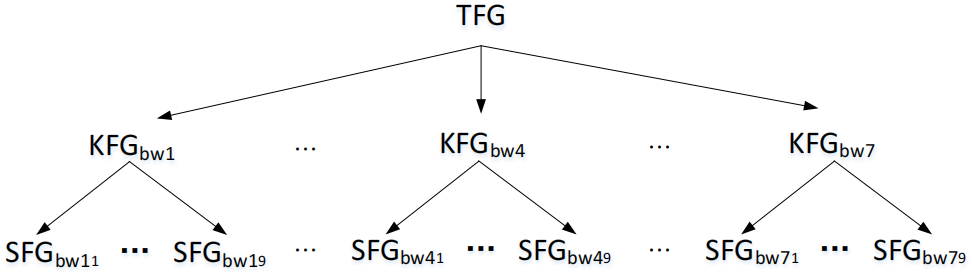
图3 Saber多项式乘法的完整因子图
BP算法消息传递包括从变量节点到因子节点uxn→fm和从因子节点到变量节点ufm→xn。
从变量到因子的消息传播:
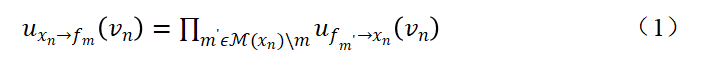
从因子到变量的消息传播:
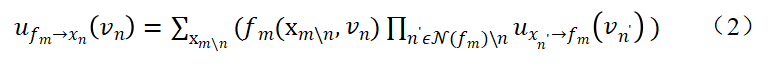
结合构建好的完整因子图,BP将上述消息规则应用于所有节点,然后通过传播迭代,得到密钥的概率分布,这样就完成了一次完整的攻击。
2、攻击优化
(1) 选用汉明重量模型
作者采用汉明重量模型构建模板而不是以所有可能的值作为模板,将原始模板数量从216∙144∙7降至17∙144∙7=17136个。
(2) 结合深度学习
作者结合深度学习,建立多层感知机架构MLP,设置隐藏层激活函SeLU、输出层激活函数Softmax,将能量波形输入训练网络,用中间值的汉明重量作为训练标签,输出概率向量。
(3) 优化因子图
作者结合Bayes定理计算边缘概率,将因子图中的节点归一化。简化后的SFG从原有的33个变量节点变为2个,降低了BP的时间和内存复杂性。
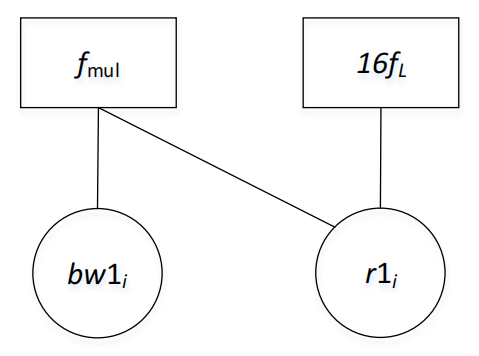
图4 基于Bayes的SFG
(4) 改进BP算法
在KFG中有很多长度为4的循环,且都与因子f5add相连。由于短周期循环十分影响BP算法的性能,因此将与f5add相关的节点与其他节点剥离开,整个环状BP分为两个步骤依次执行,以减轻性能下降。
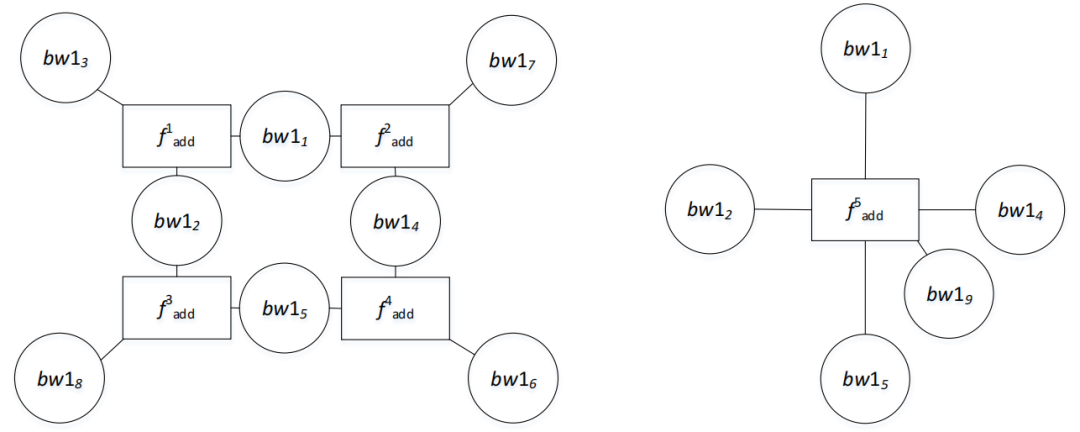
图4 KFG上的改进BP算法
实验结果
作者基于Saber的C语言实现进行模拟实验,证明了上述优化方法的有效性:(1)在成功率相同的情况下,贝叶斯SFG所用时间约为原始SFG时间的1/2甚至更低;(2)改进BP算法的攻击成功率优于传统BP算法,同时减少了攻击时间;(3)基于深度学习的SASCA比传统模板攻击的SASCA成功率更高。
进一步地,作者对STM32 Nuncleo-64板上的STM32F103RB(ARM Cortex-M3)电磁辐射控制器进行实际攻击,验证了攻击的实用性。
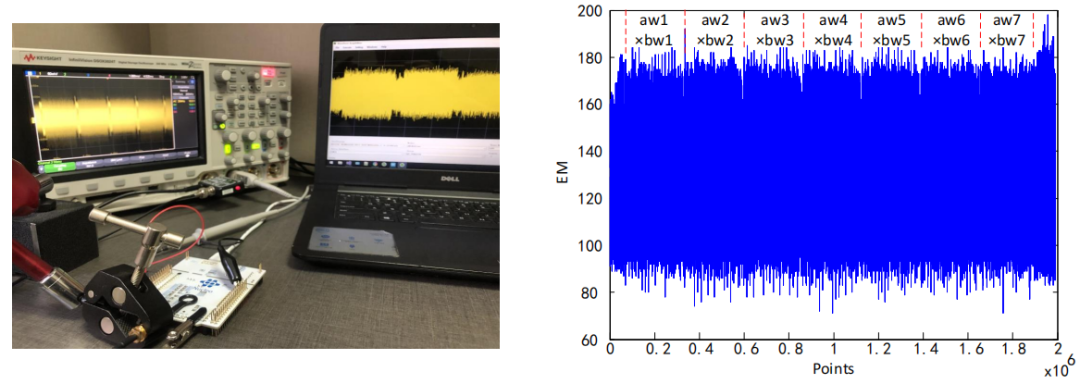
图5 实验设备与电磁波形
结论
作者展示了如何使用SASCA攻击Saber中的Toom-Cook乘法,并进一步结合深度学习优化攻击,减少传统SASCA的模板数量。同时基于贝叶斯定理将因子图中的节点归一化,简化了SFG;改进BP算法,降低因子图中短周期对BP算法的性能影响,实现了攻击优化。这些技术对其他执行Toom-Cook算法的密码方案的安全性研究起到了十分重要的借鉴意义。