简述同态加密的发展历程
前言
深度详谈系列是同态科技面向行业群体推出的专业性文章,旨在分享隐私计算及密码学相关知识、增强行业群体之间的双向交互性,打破专业壁垒、使得复杂技术及理论可触可见。
上一篇的科普文章简单的介绍了什么是同态加密,本篇文章将详细梳理同态加密技术的发展脉络,根据其发展路径,总结、归纳出同态加密算法的构造类型,讨论该技术的应用场景,最后指出其发展方向,对同态加密技术的研究具有指导意义。
01 发展历程
1978 年,Rivest 等人提出利用同态加密的思想来保护数据信息的安全性,即通过利用具有同态性质的加密函数,对加密数据进行运算,同时保护数据的安全性。
这一概念提出后,引起了众多密码专家学者们的关注,由于这个良好的性质,人们可以委托第三方(可信或不可信)处理数据,并根据该思想设计了很多具有同态性质的加密方案。
20世纪80年代,出现了大量的非紧致的同态加密技术,这些方案的构造大多采用了Yao的电路技术。
2005年,Boneh、Goh和 Nissim提出了一个支持任意次加法运算和一次乘法运算的密码方案,且过程中不会增加密文的噪声。
2007年,Melchor 等人描述了一种构造加密方案的模版,它能够计算浅层电路,且密文会随着乘法深度呈指数增长,而加法不会增长其尺寸。
同态加密算法的构造类型
根据近年来同态加密发展的路径,现有的同态加密算法的构造思想大致可以分为三类:
- 基于整数或理想格进行构建,以Gentry 等人的工作为代表为代表。
- 基于LWE或R-LWE问题构建,以Brakerski等人的工作为代表。
- 基于LWE问题,以GSW13为代表。
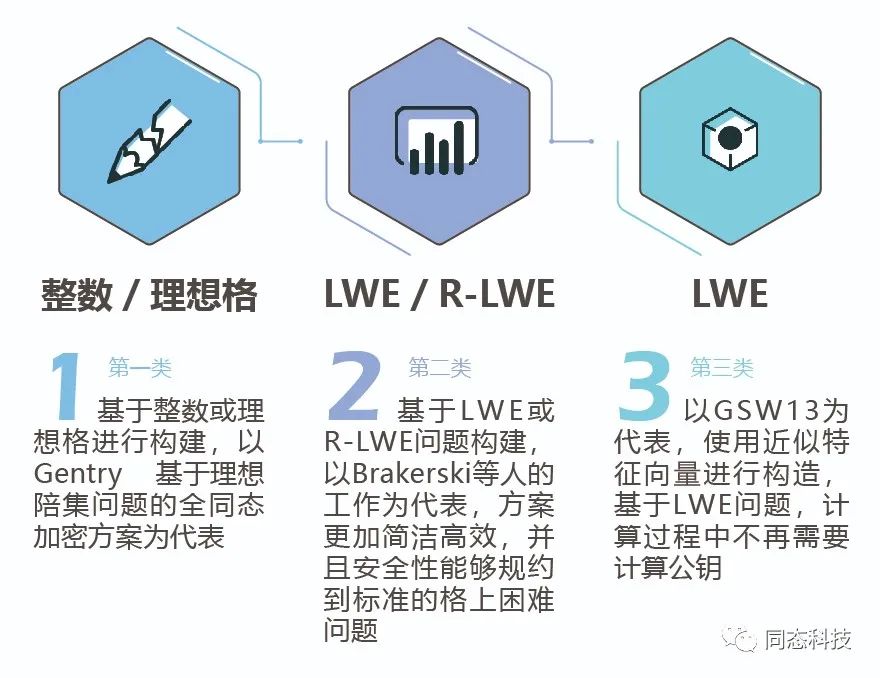
同态加密算法的三种构造类型
1.基于整数或理想格理论来进行构建,需要使用bootstrapping技术来实现全同态加密方案。
2009年,全同态加密的历史上出现了一个里程碑式的节点,Gentry构造出了世界上第一个全同态加密方案。最初Gentry 的实现采用了理想格,基于理想陪集问题进行设计,现在还有很多方案思想都是源于Gentry的方案。
2010年,Dijk、Gentry及Vaikuntanathan又提出了一个基于整数的全同态加密方案。基于近似最大公因数问题进行设计,原始方案仅仅支持低阶多项式的运算。而在使用了早先提出的bootstrapping技术之后,该方案能够进行密文刷新,从而使得算法能够支持更深的计算电路。
bootstrapping技术是一种密文的刷新技术,可将任何能够运算自身解密电路的同态方案转化成全同态方案,常被用于构造深度为d的全同态加密方案。
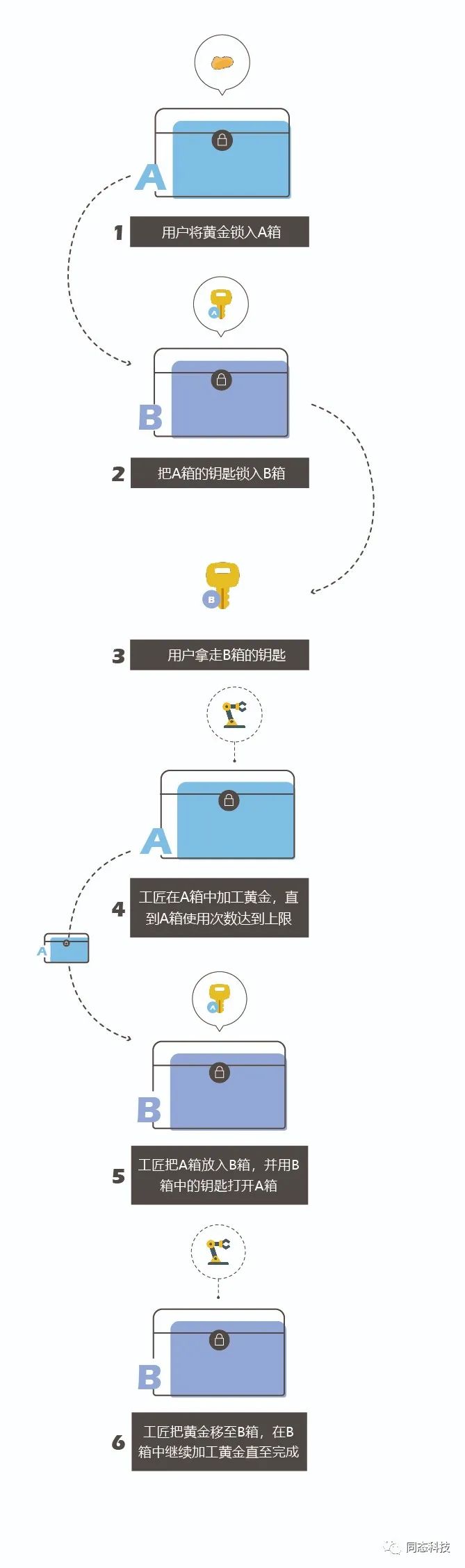
bootstrapping技术的原理可以通过黄金操作箱的例子来说明:
A/B黄金操作箱
假设所有的操作箱操作黄金的次数都是有限的,没有办法通过操作箱的方式将黄金加工成复杂的工艺品。
现在,为了实现复杂工艺品的加工,有人提出了一个很巧妙的办法:
如果事先可以知道需要对黄金操作的次数的话,那么通过准备多个箱子,就可以实现更加复杂的操作。
2基于格进行设计,其安全性依赖于LWE以及R-LWE问题,效率上和第一类算法相比,具有极大的提升。
2011年,Brakerski和Vaikuntanathan提出了一个基于标准格上困难问题LWE的同态加密技术。
该方案首次使用标准格上困难问题构造了全同态加密,利用“重线性化”技术,在不引入理想相关假设的条件下,构造了一个部分同态加密方案。
其次,该方案又利用“dimension-modules reduction”技术,缩短同态密文,在不需要”squashing”和稀疏子集合假设的条件下,将部分同态加密方案扩展为全同态加密方案。
2012 年,Brakerski 等人共同构造了 BGV12方案,利用密钥转换(Key Switching)技术以解决密文进行乘法运算后的膨胀问题,并利用模转换(Modulus Switching)技术以抑制密文运算中增长的噪声,可使 SWHE方案(部分同态加密,支持加法和有限次乘法)方案转换为层次型同态加密方案(也可近一步使用 bootstrapping 转化为 FHE 方案)。
这是一个重大的转折:打破了原有的 Gentry 框架,在效率上有了质的飞跃。在接下来的几年中,多个密码学者陆续提出了对同态计算效率进行优化的技术,如将多个明文比特“打包”到一个密文中,以及多个对 bootstrapping 过程进行改进优化的方案。
同年,Brakerski还提出了Bra12方案,在方案中,提出了一个基于LWE问题的同态加密方案的通用噪声压缩算法,使得噪声增长从 缩减为 。
2017年,Cheon等人提出了一个能够兼容浮点数,并对浮点数进行运算的全同态加密方案CKKS。
Cheon等人使用了一种近似规约技术。在此过程中,明文被近似取整,而密文被截断(truncates)为若干较小的模数,在解密后进行重组,并被还原为小数。
2019年和2020年,Cheon又提出了针对同态密文的max和min函数计算方法。
3以GSW13为代表,使用特征向量构造全同态加密方案,使用近似特征向量进行构造,计算过程中不再需要计算公钥。
2013 年,Gentry、Sahai 和 Waters基于 LWE 困难问题构造全同态加密方案GSW13,使用了近似特征向量方法,构造了矩阵形式的层次型同态加密方案。
密文是矩阵形式,且私钥是密文矩阵的近似特征向量,而明文是相应的特征值。密文的同态乘法和加法分别对应矩阵的乘法和加法,这避免了在之前的方案中,由于密文乘法造成的维数膨胀的问题。
该方案不再需要密钥转换技术和模转换技术,但是在运行效率上低于其他的BGV12 类方案。通过使用特征向量构造全同态加密方案,安全性可以规约到LWE问题上。
在运算时,虽然该方案不再需要运算公钥,但是计算效率与第二类算法相比,有所降低。
02 前景展望
同态加密技术虽然起步较晚,但是由于其具有可基于密文计算这一特性,因而被广泛的应用在外包计算、隐私保护机器学习、安全多方计算、联邦学习以及数据交换共享中,从而吸引了大量的专家学者对其进行研究。
目前,针对同态加密技术的研究主要集中在提升计算速度、缩短密文长度、扩展数据类型以及扩展所支持的操作等方向。
随着技术的愈发成熟,相信在不久的将来,同态加密一定能够得到更加广泛的应用。
参考文献
[1] Gentry C. Fully Homomorphic Encryption Using Ideal Lattices. In the Proceedings of the 41st Annual ACM Symposium on Theory of Computing (STOC 2009). Bethesda, MD, USA. May 31-June 2, 2009.
[2] Brakerski, Z. (2012). Fully Homomorphic Encryption without Modulus Switching from Classical GapSVP. Advances in Cryptology – CRYPTO 2012:868–886.
[3] Brakerski, Z., Gentry, C., & Vaikuntanathan, V. (2012). (Leveled) fully homomorphic encryption without bootstrapping. ACM Trans. Comput. Theory 6, 3, Article 13,2014:13-48.
[4] Van Dijk M, Gentry C, Halevi S, Vaikuntanathan V. Fully homomorphic encryption over the integers. Advances in Cryptology-EUROCRYPT 2010, Springer Berlin Heidelberg, 2010: 24-43.
[5] Brakerski Z, Gentry C, Vaikuntanathan V. (Leveled) fully homomorphic encryption without bootstrapping. Proc of the 3rd Innovations in Theoretical Computer Science Conference. NewYork: ACM, 2012: 309-325.
[6] Gentry C, Halevi S, Smart N P. Better Bootstrapping in Fully Homomorphic Encryption. International Conference on Practice and Theory in Public Key Cryptography. Springer-Verlag, 2012:1-16.
[7] Paillier P. Public-key cryptosystems based on composite degree residuosity classes. EUROCRYPT 1999, 1999, 547(1):223-238.
[8] Cheon, J. H., Kim, A., Kim, M., & Song, Y. Homomorphic Encryption for Arithmetic of Approximate Numbers. Lecture Notes in Computer Science, 2017:409–437.
[9] Brakerski Z, Vaikuntanathan V. Efficient fully homomorphic encryption from (standard) LWE[C]. Proc of the 52nd Annual Symposium on Foundations of Computer Science. Washington DC: IEEE Computer Society, 2011: 97-106.