ACM TDS'22：深度学习中基于扰动的梯度下降优化方法

深度学习在各个领域取得巨大成功，其成功与海量数据的提供密切相关。 但一般而言，大数据集中包含丰富的敏感数据，因此模型训练应该具有避免隐私泄露的能力。 为实现该目标，许多工作将差分隐私应用到深度学习中以保护训练阶段的模型隐私。 针对该问题，本文提出一种新的扰动迭代梯度下降优化算法(PIGDO)，并证明其满足差分隐私的标准。 此外，本文还提出一种改进的矩统计方法(MMA)以进行隐私分析，与原有矩统计方法相比，MMA统计方法能够获得更为严格的隐私损失上界。 实验结果表明，PIGDO算法不仅能提高模型的准确度和训练速度，而且在达 到相同准确度的同时，比现有算法具有更好的隐私保护能力。

该成果“Differentially Private Deep Learning with Iterative Gradient  Descent Optimization ”发表在ACM/IMS Transactions on Data Science， 2022。 ACM/IMS Transactions on Data Science是数据科学领域综合性期刊。

• 论文原文：
• https://dl.acm.org/doi/pdf/10.1145/3491254

背景与动机

深度学习在取得巨大成功的同时，其安全问题也广受关注。 最近的研究表明，训练有素的机器学习模型仍容易受到隐私风险的影响。 因此，在利用深度学习时有必要考虑隐私保护问题。 与其他的隐私保护方法相比，在攻击者具有最大背景知识的情况下，差分隐私能够抵抗各种类型的攻击。 继经典的差分隐私SGD算法提出，已有许多后续工作利用各种技巧来提高梯度扰动后的模型准确度，同时达到令人满意的隐私保护效果。 主要的改进方法包括两类： 一类通过研究每个梯度分量的灵敏度以添加依赖于灵敏度的噪声来获得更高的模型准确度。 另一类使用的改进策略是基于不同特征和模型输出之间的相关性，自适应地向梯度中注入噪声。 然而，基于灵敏度分析的梯度扰动法通常需要求解高维灵敏度约束条件，这在深层神经网络中是难以解决的。 类似地，基于 相关度分析的梯度扰动法需要在不同神经网络层中计算每个特征的相关度，这将导致计算效率低下。虽然这两类方法都是为每个梯度分量或每个神经元梯度添加适当的噪声而设计，但它们对实现可行而高效的隐私保护学习算法提出更为严格的要求。

因此，考虑到上述 梯度扰动机制的局限性，我们从全局的角度来对现有梯度扰动方法进行改进。此外，大多数现有的深度学习工作，在实现差分隐私时都采用DPSGD来控制训练数据对训练过程的影响。然而，SGD算法有其固有缺点，如难以逃脱鞍点和选择合适的学习率。这些缺 点可通过自适应梯度下降优化算法来克服，因此我们选择梯度下降优化算法来进行深度学习训练。 理论上，梯度下降优化算法提供比传统SGD更好的收敛速度，而且其具有如自适应动量等性能优势，能够克服传统SGD算法的缺点。 最后，在上述分析的基础上，我们将梯度下降优化算法整合为迭代分量，并在该分量中注入适当的噪声，以达到更好的整体模型效用。

设计与实现

本文提出一种基于扰动的迭代梯度下降优化算法（PIGDO）来实现差分隐私。 该算法框架适用于广泛使用的ADAM、Adagrad和RMSprop三种自适应梯度下降优化算法。 具体而言，在该算法中，我们首先引入一个专门针对差分隐私深度学习的训练参数： 批量大小 L。 批量大小的引入是用于合理地增加噪声，它不同于传统机器学习中用于方便计算的批次概念。 随后，我们成批地执行计算任务，将一些小批量聚合成大批量以添加合适的噪声。 通过从样本中随机选取大量样本以进行迭代，并利用梯度下降优化算法计算所选样本上损失函数的梯度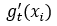 。 其次 ，考虑到梯度下降过程中，梯度可能会变得很大，根据灵敏度定义，这样很难得到有用的梯度灵敏度，因此为实现差分隐私学习算法带来挑战。 为克服这一困难，可以采用梯度裁剪，即用阈值C 对梯度 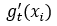的L₂ 范数进行裁剪以限定每个样本的梯度。 换言之，用 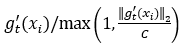替换 每个梯度 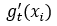以将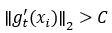 降至范数C 。 之后，计算这些裁剪梯度的平均值，并将随机噪声 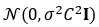添加至该平均值 以实现噪声扰动。 最后，在每一步迭代中使用噪声梯度 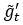来更新模型参数。 由于每步迭代都满足差分隐私，基于其组合性质，最终的模型参数也将满足严格的差分隐私标准。

除输出模型参数外，噪声的添加使得本算法的隐私损耗上界分析成为另一大关键挑战。因此，我们以PIAdam为例，具体分析如何计算差分隐私梯度下降优化算法的隐私损失。值得说明的是，该理论分析过程同样适用于其他 差分隐私梯度下降优化算法的 隐私性能分析。在基于扰动的深度学习算法中，为得到训练良好的差分隐私深度学习模型，通常需要经过多次迭代训练，这些迭代组合步骤最终会导致较大的整体隐私损失。因此，需要提出合适的隐私损失计算方法 来解决该问题。已有一 些方法来对隐私损失进行统计，最新的技术是根据随机变量中矩的概念来对随机隐私损失函数进行度量，并提出矩统计方法以对多次组合的隐私变量进行累积计算。该方法比传统的强组合定理实现更紧致的隐私损失估计。然而在矩统计方法，其对总体隐私损失进行等价无穷小变换，导致最终的隐私上界变得宽松。针对该问题，本文在理论计算中保留原始总体隐私损失并给出严格定理，以证明PIAdam满足差分隐私。从最终结果可知，本文的隐私损失上界不仅具有便于计算的明确表达式而且实现比原先的矩统计方法更为紧致的上界。

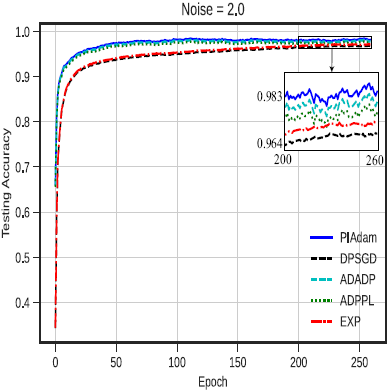
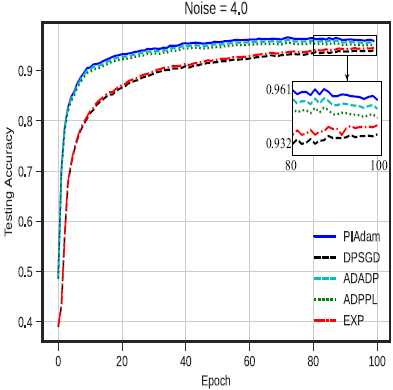
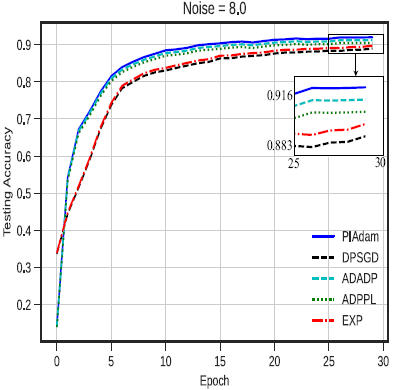
为进行实验评估，我们进行三个流行的图像分类任务，包括MNIST手写数字识别、CIFAR-10图像分类和Fashion-MNIST服装图像分类。 本实验设置下的MNIST非隐私模型训练/测试准确率达到98.62%/98.57%，表明本实验设置下的神经网络结构能够实现与最新模型相当的性能。 CIFAR-10的非隐私模型可以达到86%的测试准确度。 Fashion-MNIST是一种新的数据集，可以看作是MNIST数据集的替代，其非隐私模型训练/测试准确率达到97.94%/88.85%。 在三个数据集上，我们将差分隐私梯度下降优化算法PIAdam与现有的ADPPL、 ADADP（INFOCOM'20）、EXP（S&P'19）和DPSGD（CCS'16）算法进行比较。在准确性方面，下图给出具有不同隐私级别的三种情况下的训练结果：对应于 大噪声级别的高隐私级别（σ=8）、对应于中等噪声级别的中隐私级别（σ=4）和对应于小噪声级别的低隐私级别（σ=2）。 在每个图片中，我们给出PIAdam、ADADP、ADPPL、EXP和DPSGD的测试准确度，这些测试准确度随着时间的变化而变化。 结果表明，PIAdam在所有级别的测试准确度上都超过或大致相当于其他算法。 当噪声为8时，PIAdam的测试准确率高达92.02%，比ADADP(91.25%)、ADPPL(90.92%)、EXP(89.75%)和DPSGD(88.91%)分别提高了0.82%、1.65%、2.5%和3.48%。 同样，当噪声σ=4时，PIADAM的测试准确率达到95.93%，接近ADADP的95.43%； PIADAM仍比ADPPL(94.94%)、EXP(94.54%)和DPSGD(94%)分别提高1.05%、1.47%和2%。 在噪声为2时，PIADAM的测试准确度达到98.21%，比ADADP、ADPPL和EXP提高了1%以内，但仍比DPSGD(96.81%)提高了1.44%。 可以证明， 本文所提基于扰动的迭代梯度下降优化算法比DPSGD（CCS'16）等工作获得更好的准确度。

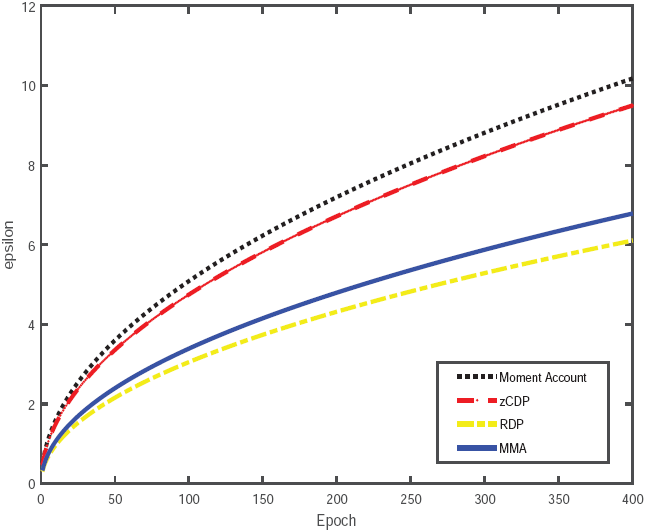
在隐私损失计算方面，下图给出隐私损失随时间变化的四条曲线，它们分别对应于矩统计方法MA、zCDP、RDP和所提的改进矩统计方法MMA。 由图可知，本文提出的MMA方法总是比矩统计和zCDP方法具有更低的隐私损失。 此外，MMA方法的隐私损失比矩统计和zCDP方法增长得更慢。 这意味着对于给定的总体隐私预算，本文的方法允许执行更多的训练次数，这通常会实现更高的模型准确度。 总体而言，本文的优化方法在隐私保护和模型准确性方面都更加有效。

详细内容请参见：

Xiaofeng Ding, Lin Chen, Pan Zhou, Wenbin Jiang, and Hai Jin, "Differentially Private Deep Learning with Iterative Gradient Descent Optimization," ACM/IMS Transactions on Data Science, vol. 2, no. 4, pp. 1-27, 2022. 

https://dl.acm.org/doi/pdf/10.1145/3491254