针对流密码的侧信道攻击

状态或密钥恢复的三步方法

背景介绍

对称密钥密码学是保证当今通信安全的基石之一，且对称密钥密码通常比非对称密钥密码效率更高，因此，只要通信协议允许，使用对称密钥密码会更好。而侧信道攻击是针对对称密码安全性的一个重要手段，已经引起了密码学领域的高度关注。但是，分组密码(和类似的结构)似乎一直都是人们关注的焦点，而对称密码的另一个主要分支——流密码(和类似结构)，却没有被充分分析。

本文在CHES 2021破解LFSR方法（DAPA）的基础上，提出了一种通用的恢复流密码状态或密钥的自动化框架工具并开源^[1]。

攻击方法

本文主要用到的技术包括MLP、MILP（Mixed Integer Linear Programming）以及SMT（Satisfiability Modulo Theory）。攻击方法如下图所示：

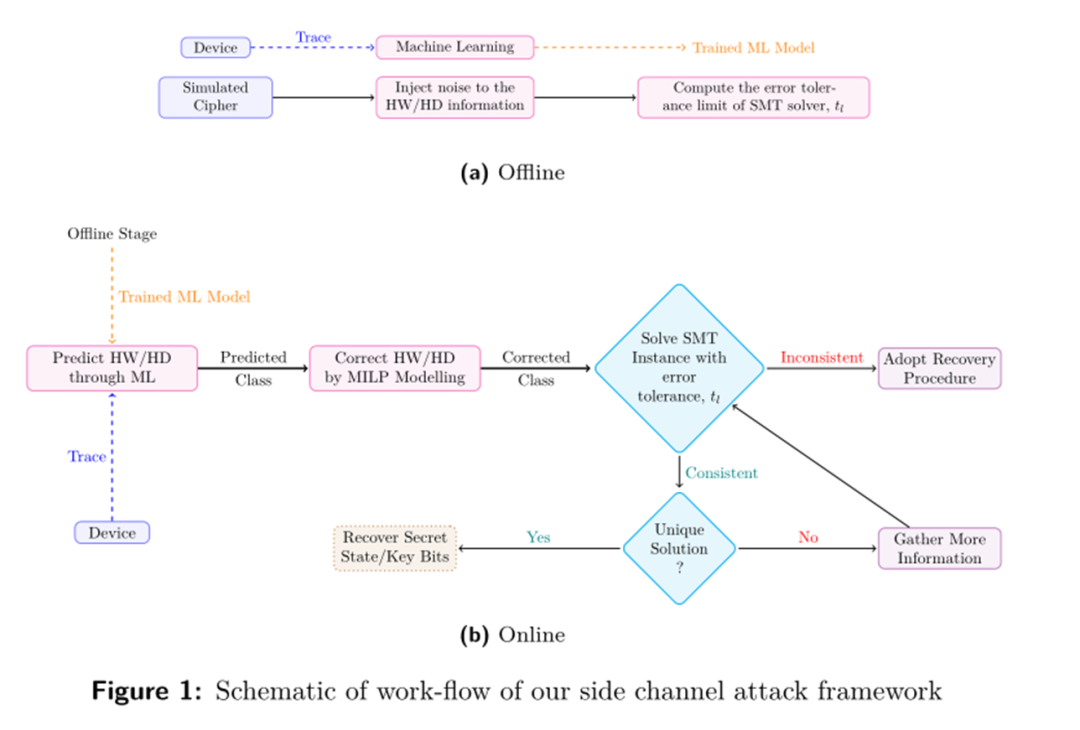
图1 攻击方法流程图

本文攻击方法主要包括Offline及Online两个阶段，其中Offline阶段包括：

• 得到分好类的波形；
• 对ML进行训练；
• 测试SMT(可满足性模理论)得到容忍度ε。

其中Online阶段包括：

• 用训练好的ML进行分类；
• 增加错误容忍度ε；
• MILP加约束修正；
• 用SMT返回猜测的中间状态或密钥。

1、ML分类

图2为错误容忍ε的大小与ML的准确率及SMT求解时间的关系。可见，随着错误容忍ε越来越大，ML的准确率越来越高，但SMT的求解时间也越来越大，甚至到最后会无法接受，故需要选择合适的错误容忍ε。

图2 错误容忍ε的大小与ML的准确率及SMT求解时间的关系

2、MILP修正

经过训练好的ML对波形进行分类后，若直接输入到SMT中进行求解，求解时间依旧会很长，甚至会出错，此时，本文通过先将波形分类进行MILP修正，再输入到SMT中，大大减小了求解时间，并提高了正确率。

其中，MILP修正具体参考了一些限制准则，如：

（1）HW的变化；

（2）运算块之间的相互作用。

此外，寄存器变化上下限、Block变化上下限以及2个块之间的变化限制都可以作为MILP修正的依据对波形分类进行修正。

3、SMT求解预测

SMT求解预测流程如下图3所示:

图3 错误容忍ε的大小与ML的准确率及SMT求解时间的关系

实验

本文针对国际标准流密码算法TRIVIUM对上述方法平台进行了实验验证，实现对象为Arduino开发板上的ARM Cortex M3 32-bits，并利用网格SNR的方法采集了SNR最高地方的电磁信息(使用了Riscure探头、Lecroy示波器)。其中ML选择了MLP模型，共使用了2362000条波，MILP采用的是Gurobi，SMT采用的是Z3。

其中一次实验结果如下图所示，通过平均时间可见方法效率很高：

图4 实验结果

总结

本文设计并实现了一个实用的框架，针对流密码或相关结构的密码算法，从侧信道信息(功率或EM)来恢复状态/密钥。本文的框架能够攻击初始化阶段(即在密码到达伪随机阶段之前)，更重要的是，甚至在密码到达伪随机阶段之后也能攻击生成密钥流。本文还通过在32位软件平台上实现流密码TRIVIUM算法，并进行电磁分析，证明了框架的有效性。

参考资料

[1] Satyam Kumar, Vishnu Asutosh Dasu, Anubhab Baksi, Santanu Sarkar, Dirmanto Jap, Jakub Breier, Shivam Bhasin:Side Channel Attack On Stream Ciphers: A Three-Step Approach To State/Key Recovery. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2022(2)CCF none: 166-191 (2022)