抗量子计算的密码就一定安全？

背景介绍

众所周知，目前使用的公钥加密算法都是基于某个数学困难问题，比如大整数分解问题和离散对数问题。但是一旦大型量子计算机研制成功，这两个问题可以通过肖算法得到有效的解决。因此美国国家标准与技术研究院(NIST)在多年前发起了征集后量子时代密码算法的项目。

NIST后量子时代标准化项目目前进行了三轮。第一轮主要关注算法在安全性上的评估；第二轮主要考虑算法的具体实现；第三轮关注算法在侧信道攻击下的安全性。

第三轮评审的四个候选算法中有三个都是基于格理论的算法，分别是基于NTRU方案的候选者NTRU，基于Learning With Errors(LWE)方案的Kyber和基于Learning With Rounding(LWR)方案的Saber。这三个算法的困难性都来源于向线性方程中插入未知噪声。

在2021年的学术会议CHES上，Kalle Ngo等人实现了针对带掩码IND-CCA安全的Saber KEM算法实现的侧信道攻击。应用神经网络学习高阶模型，不需要知道随机掩码值，并且在建模阶段不需要一个可以被完全控制的分析设备。其中，带掩码IND-CCA安全的Saber KEM算法由Michiel等人于2020年提出，该算法的开销是无掩码版本的2.5倍^[1]。

泄露分析

论文首先介绍了Saber的公钥加密算法和密钥封装算法，具体算法过程如图1和图2所示。

图1 Saber公钥加密算法

图1中是Saber的公钥加密算法，同一般的公钥加密算法，用户需要生成一对公私钥，发送方使用公钥加密要传递的信息，接收方收到信息后使用私钥解密。

图2 Saber密钥封装算法

图2是Saber的密钥封装算法，其中应用了图1中的公钥加解密算法。密钥封装算法一般是用于传递对称加密算法的密钥，其相比于直接用公钥加密算法有效率上的优势。这篇论文攻击的是密钥解封算法，具体就是图2的第1行代码。

论文提出了两个问题，第一个问题是如何确定泄露位置，第二个问题是如何在不知道掩码的情况下恢复信息message(也就是图2中密钥解封算法第一行的m')。

对于第一个问题，论文提出的解决方案是根据无掩码的实现方案确定若干大概位置，对于每一个大概位置使用深度学习模型进行学习，如果模型可以学习到一个很高的准确度，则认为这些点有泄露，否则就平移窗口并重复训练。

对于第二个问题，在目前场景下，message是一个256比特的数，每个比特是0或者1。对于message的每一个比特m，一阶掩码会将其分为两个分量r和m⨁r。在训练阶段，模型将两个分量对应的波形共同作为输入，将m的值作为标签。在攻击阶段，模型将两个分量对应的波形共同作为输入，输出一个概率值，代表该比特为1的概率。

由于公钥加密算法可以预计算一组对应于随机或者选择message的密文，因此本论文的攻击方法可以在训练阶段在被攻击设备上采集能量迹作为训练集。

图3是Saber带掩码和不带掩码的解密算法源码，其中标红的代码是存在泄露的代码。

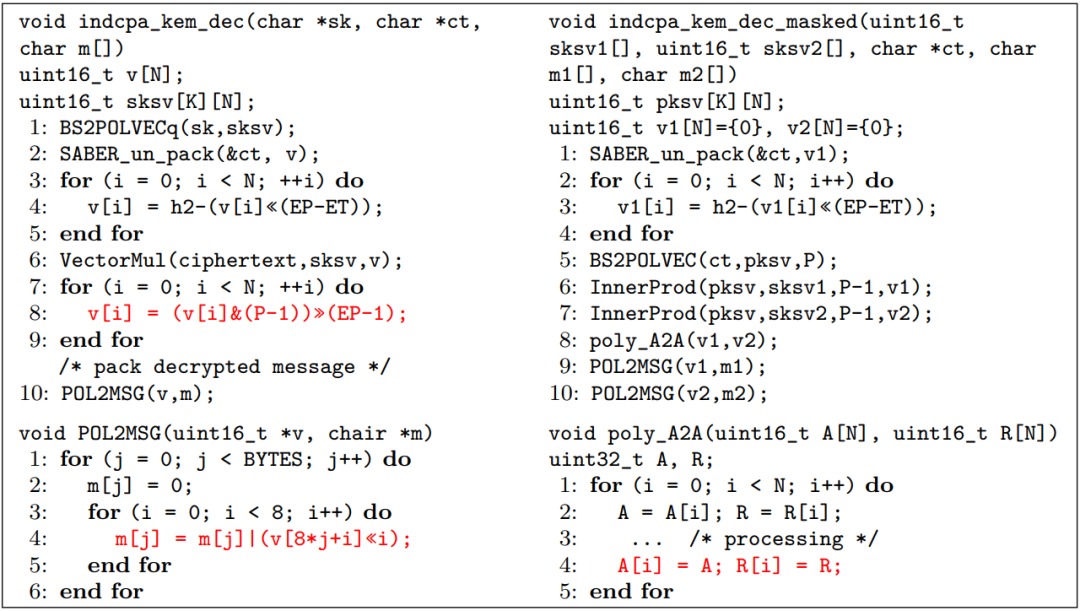
图3 不带掩码和带掩码的Saber解密算法的C源码

可以看到，带掩码的解密算法存在两种泄露，第一种泄露是在其第8行代码，poly_A2A函数将带掩码的中间值的两个分量作为输入，对其逐比特进行操作。第二种泄露是在其第9和10行代码，POL2MSG函数的功能是将比特数组转换为字节数组，因此也存在泄露。

实验环境与攻击模型

图4是这篇论文的实验环境，包括一个ChipWhisperer-Lite板子，一个CW308 UFO板子和一个CW308T-STM32F4目标板。其中D1、D2和D3都是同一种芯片，但是D1和D2是同一厂商生产的芯片，D3是另一厂商生成的芯片。

图4 用来采集能量迹的设备以及三种实验中使用的板子

论文的攻击模型取决于攻击者拥有的攻击时间长短。如果攻击者有充足的时间在被攻击设备上采波，则训练集和测试集均来源于被攻击设备，在这种情况下，D1用来训练和攻击；如果攻击者的时间只够用来采集攻击波形，则攻击者需要另一台类似设备用来建模。在这种情况下， D1用来建模，D2和D3用来攻击。

实验过程与结果

在实验的建模阶段，采集若干能量迹，按照字节或者比特进行切分，因其是带有一阶掩码防护的能量迹，因此通过将两个分量对应的能量迹进行组合，可以将训练集扩大32(按字节分段)或者256倍(按比特分段)。

对于poly_A2A函数的泄露，训练一个模型即可，对于POL2MSG函数的泄露，由于用一个字节需要连续异或8个比特，每次异或时其余的比特状态不同，因此需要训练8个模型。

因为论文数据集中的能量迹在时间轴上非常整齐，因此作者发现MLP的效果要比CNN更好，所以论文最终使用的是MLP。

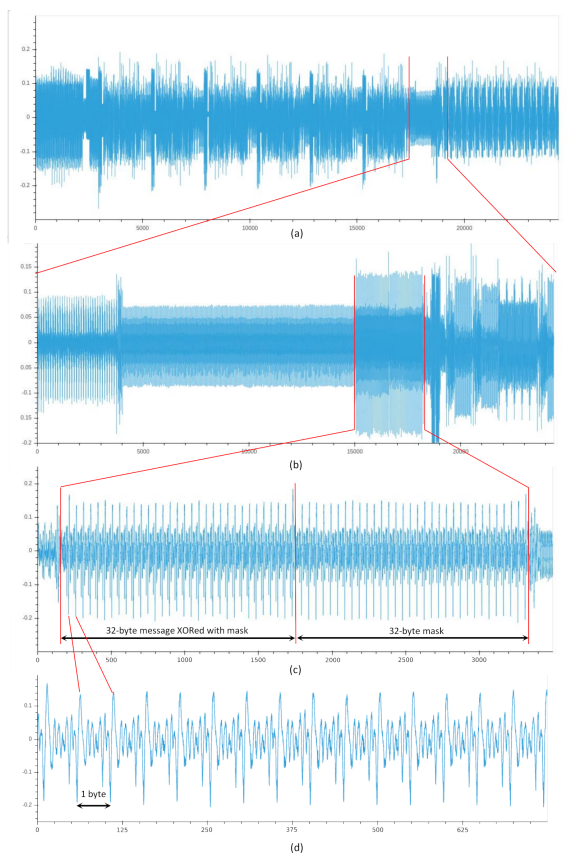
图5(a)Saber密钥解封部分的初始能量迹；(b)包含poly_A2A(v1，v2)，POL2MSG(v1，m1)和POL2MSG(v2，m2)的能量迹；(c)POL2MSG的两个分量；(d)第一个分量的前15字节。

图5是原始能量迹。论文作者首先根据无防护版本算法的经验确定了一个大概的位置，根据poly_A2A函数中有一个大小为256的循环和POL2MSG函数中有一个大小为32的循环，确定了它们的具体位置。

图5(c)是带掩码的中间值的两个分量对应的能量迹，论文作者通过将两个分量对应的能量迹按字节进行切分，并将对应字节的能量迹进行拼接，构造了神经网络的训练和测试集。

训练阶段，从D1上采集了50K条波，随机密文和密钥。对于poly_A2A函数的泄露，构建了4K×256=1.024M训练集，对于POL2MSG函数的泄露，构建了50K×32=1.6M训练集。测试阶段，从D1，D2和D3上分别采集了1K的波形作为测试集，测试集是随机密文和固定密钥。

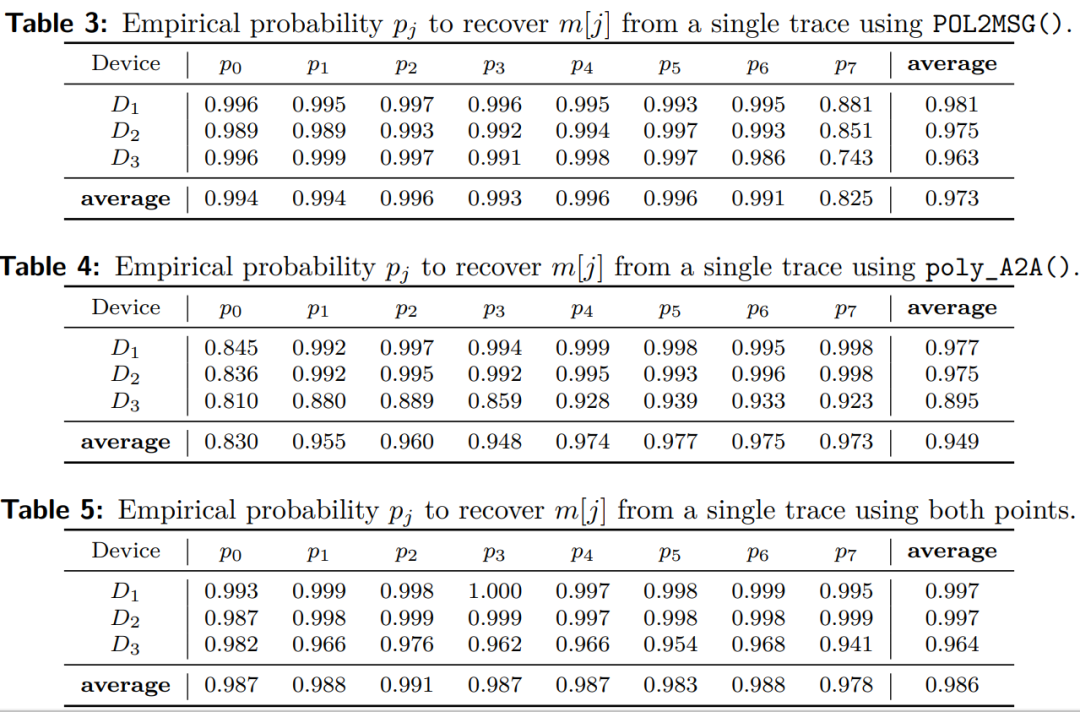
图6 论文实验结果，从上到下分别是只使用POL2MSG函数的泄露的结果，只是用poly_A2A函数的泄露的结果和两个函数的泄露都使用的结果。

图6是论文中实验结果的截图。分别是只使用POL2MSG函数的泄露结果、只使用poly_A2A函数的泄露结果和使用两个函数的泄露结果。

由实验结果发现，对于POL2MSG函数的泄露，第7个比特最难攻破，对于poly_A2A函数的泄露，第0个比特最难攻破。

为了解释这一现象，论文对波形做了TVLA和SOST测试。结果如图7和图8所示。

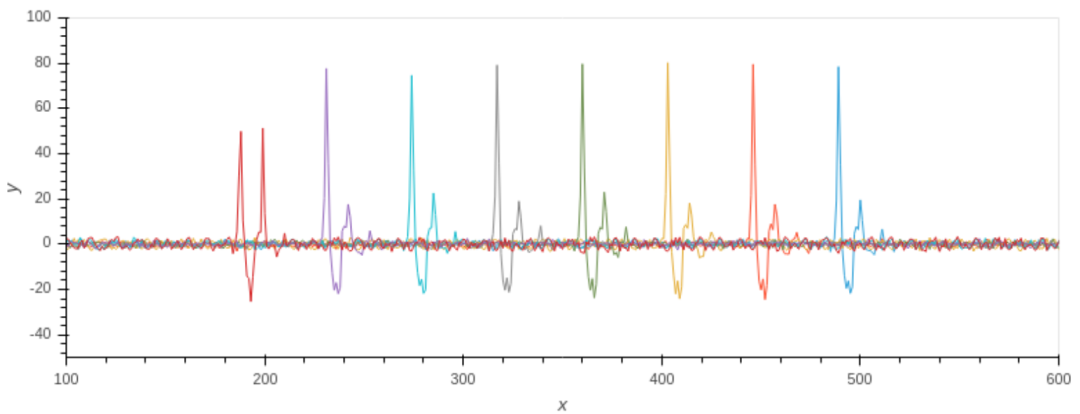
图7 m⨁r分量的第一个字节的poly_A2A泄露和POL2MSG泄露的t-test结果

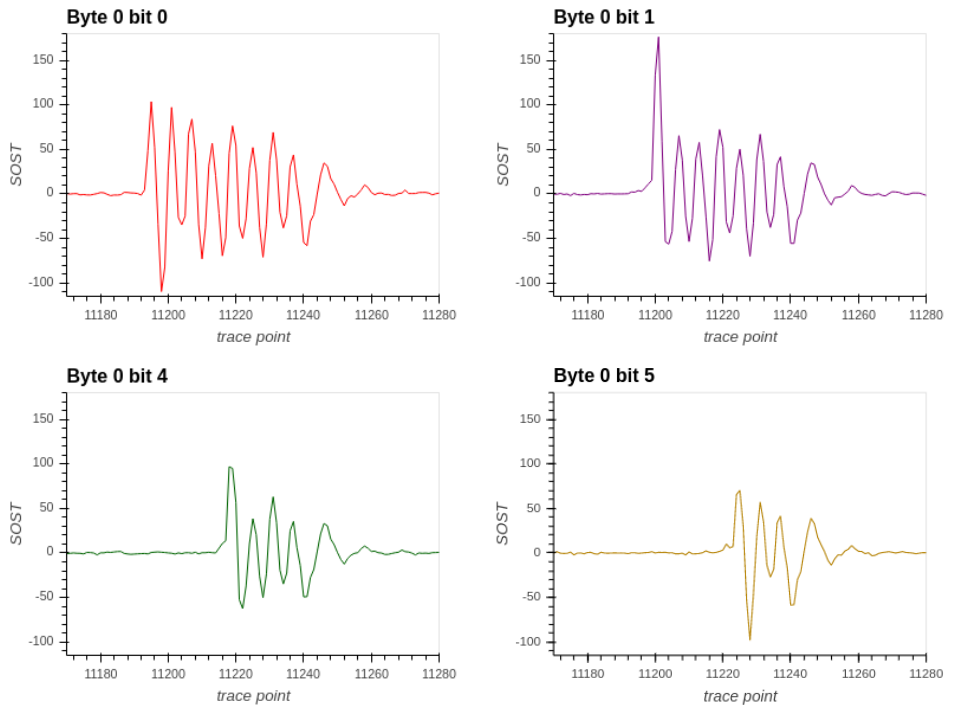
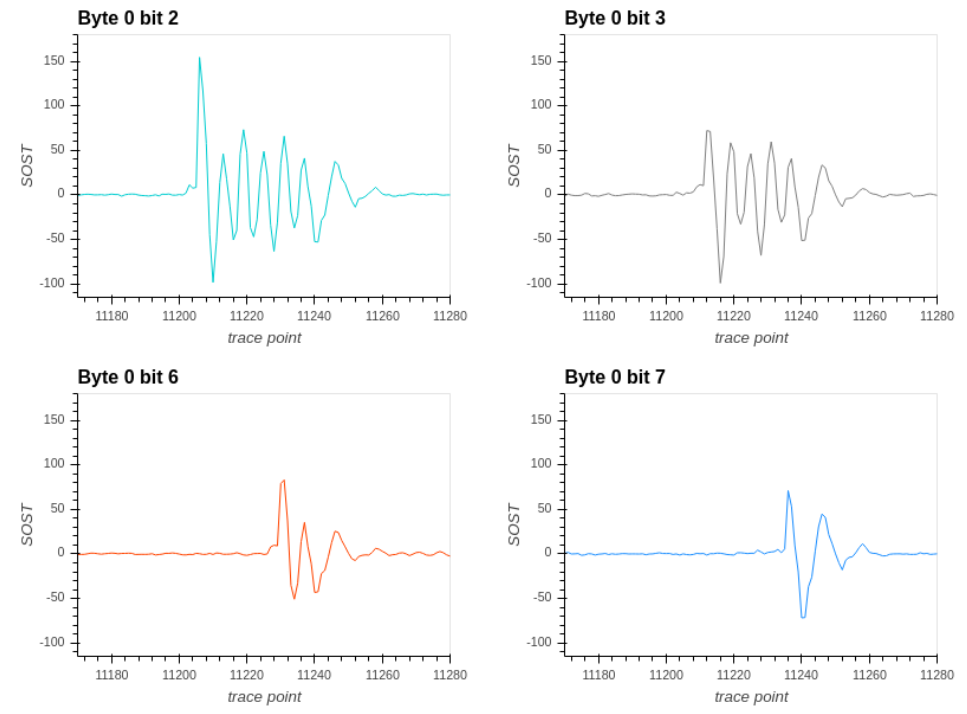
图8 POL2MSG泄露逐比特的t-test结果

论文作者分析后认为，对于poly_A2A泄露，只有第一个比特前的操作和其它比特不同，因此导致了第一个比特的泄露比其它比特低；对于POL2MSG泄露，越靠后异或的比特位的能量泄露越小。

在成功恢复出中间值message后，论文据此恢复出了密钥。

总结

作者使用了24条能量迹恢复出了带掩码的Saber算法的密钥，提出了模型的训练过程可以在被攻击设备上进行，发现了先前从未发现的泄露类型，并且在密钥恢复阶段展示了一种新的密钥恢复方法可以抵消在中间值恢复时的一些错误。