对OCB算法侧信道泄漏位置的细粒度分析
背景介绍
在CHES 2022会议上,Berti等人对OCB3算法的侧信道泄漏位置进行了细粒度分析,该算法是CAESAR竞赛获胜的算法之一。首先,作者发现可以使用DPA方法对算法中的某些密码模块(初始化模块或相关数据处理)进行攻击;接着,假设上述描述的密码模块受到了保护,此时仍可以对其他的分组密码模块进行攻击,一种方法是使用未知输入的DPA攻击,更有效的方法是利用连续加密模块之间,输入的白化值的水平关系进行DPA攻击;最后,作者考虑了当所有的密码调用块都受到了保护,但针对线性操作可以进行SPA,进而获取白化值的信息,并证明恢复白化值会对OCB3算法的机密性和完整性造成威胁[1]。
OCB3算法
1、OCB3算法结构
图1为OCB3算法的结构,算法的输入为消息m,消息分为一些块mi分别使用加密块BC加密生成密文块。这里使用AES-128初始化BC,故将消息m分为128比特的mi。
用户需要输入nonce使用初始化函数,得到δ0,然后使用更新函数Inc计算其余的δi。每个消息块mi在进入BC前,都需异或上δi,在经过BC的加密计算后,再次异或δi,生成密文块。对于最后一个密文块ml,若ml是128比特,则按照正常的BC加密,若ml小于128比特,则需要经过填充的ml异或BC(δl-1⊕l*),其中l*的定义见第2节。对于认证来说,需要使用消息的校验和生成一个标签τ,具体的计算过程见图1中最后一个BC块的计算。
若对关联数据进行处理,处理方式与消息的处理方式基本一致,用关联数据块代替消息块。然而,在消息处理的情况下,δ0的初始化值取决于随机数的加密;在关联数据处理的情况下,δ0的初始化值始终为0。
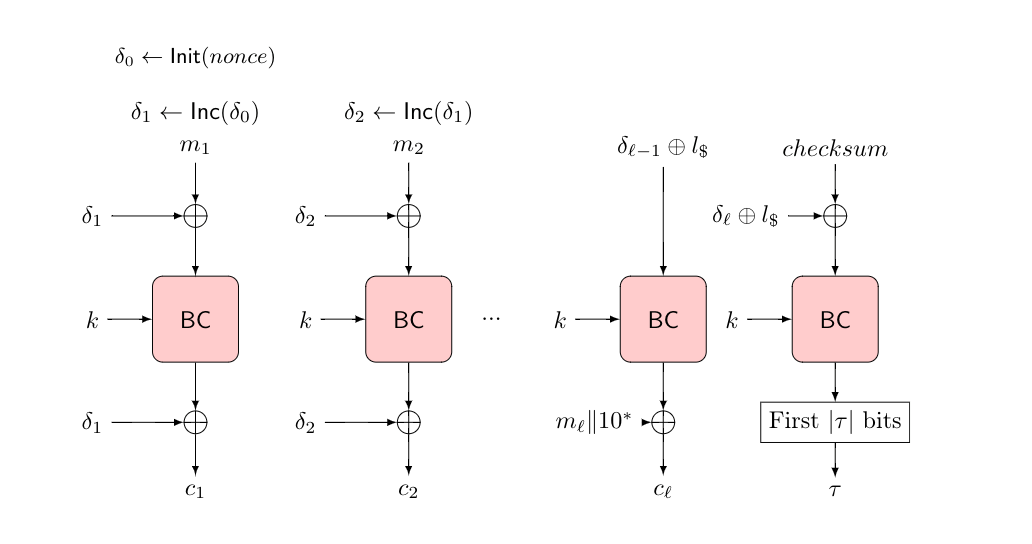
图1 OCB3算法结构
2、初始化函数更新函数
初始化函数的主要目的是生成白化值δ0,算法的主要流程如下图2所示。该算法主要分成两个部分,第一部分是通过用户输入的nonce值,计算得到中间值top。第二部分是将top输入到BC块中,使用密钥加密得到ktop。

图2 初始化函数(Init)流程
更新函数的主要算法流程如下图3所示,其中doule(x)表示在有限域上x的2倍,ntz(x)表示x的二进制表示尾部0的个数。该算法主要分为两个部分,第一部分计算得到l0=4*BCk(0),第二部分是使用初始化函数中得到的δ0,利用公式δi=δi-1⊕lnte(i)计算δi。

图3 更新函数(Inc)流程
泄漏分析
1、对无防护的OCB3算法进行侧信道攻击
(1)对OCB算法的初始化函数进行攻击:
图2为初始化函数流程,其中ktop=BCk(top)泄漏了密钥信息,可以用DPA进行攻击。在这里为了计算白化值,使用用户随机输入的nonce和密钥进行加密,其中加密块的输入是已知可控随机的,符合DPA攻击的条件。
(2)针对关联数据处理的DPA攻击:
在对关联数据处理时,δ0的初始化值始终为0,则说明第一个BC块的输入δ1始终为固定的数。则可以通过两步DPA完成攻击,第一步,攻击BC块加密的第一轮,可以得到δ1⊕k,第二步,攻击BC块加密的第二轮,得到第二轮的子密钥,推导得到密钥。
2、对安全初始化的OCB3算法进行侧信道攻击
假设在1节中描述的初始化函数中的泄漏被很好的进行了防护,作者仍找了可以进行攻击的位置,即计算密文需要的加密块BC,这里的攻击难度是BC的输入δi是未知的。
(1)基础的DPA攻击
处理这个问题最直观的想法是将δi当作掩码值进行处理,选择两处攻击位置。第一处是BC块的输入值即δi⊕mi,第二处是第一轮S盒的输出,可以得到δi⊕mi⊕k。
(2)改进的DPA攻击
在基础DPA攻击中,需要波形条数大大增加,为了降低所需的数据复杂度,提出了改进的DPA攻击。
由于δi=δi-1⊕lnet(i),故BC的输入可以全部转换为仅与δ0相关的输入,下图4为转换结果。又因为一次加密过程中的δ0是一样的,故可以将δ0作为密钥的一部分,即假设h=δ0⊕k0。在将输入转换的过程中,会产生多余的值,该部分也应该被猜测,由于li=double(li-1),故若增加l0到ln,则时间复杂度从28增加至216+n。具体的算法流程如下图5所示。

图4 BC输入的转换结果

图5 改进的DPA攻击流程
(3)实验结果
在ARM Cortex-M0上实现OCB3算法,为了更加精确,作者通过计算中间值得到信噪比SNR的值,以此确认波形中的兴趣点。分别使用基础的DPA攻击和改进的DPA攻击,得到如下图6所示的实验结果。
其中x轴为需要的波形条数,y轴为攻击成功的准确率。可以看出,使用基础的DPA攻击方法,在攻击成功率为100%时,大约需要125条波形,而改进的DPA方法,在攻击成功率为100%时,大约需要10条波形,改进的DPA方法使用的波形数量更少。
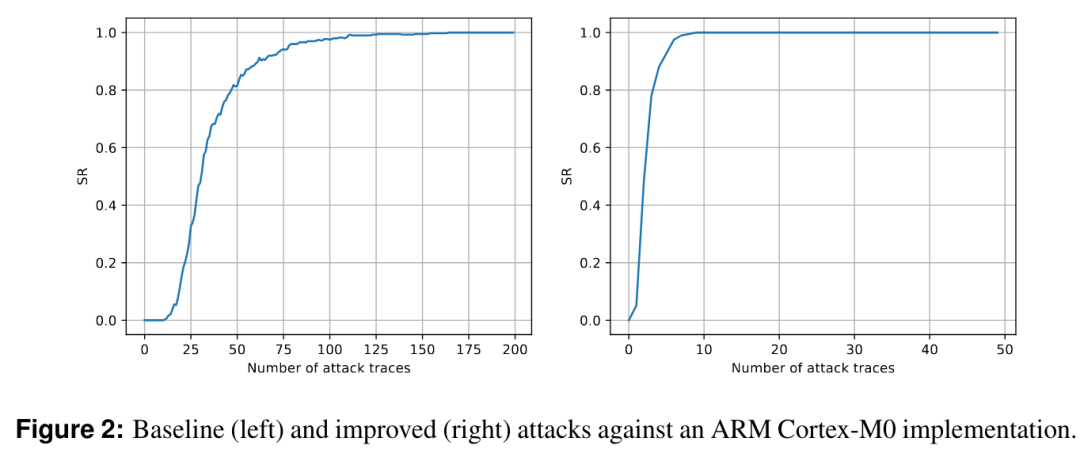
图6 两种方法进行攻击的实验结果
3、对安全加密块的OCB3算法进行侧信道攻击
当第1、2节所描述的泄漏位置均加以防护之后,即与密钥相关的计算均加上了防护,此时,无法再通过侧信道的方法获取密钥的信息。作者证明若得到OCB3算法中的l0值,会对算法的安全性和机密性造成很大的威胁,具体的证明过程见该论文的6.3、6.4节。此处不再给出详细证明过程,下面对如何使用侧信道的方法获取l0值进行介绍。
此时可以利用的泄漏位置是δi=δi-1⊕lnet(i)和BCk(input)=δi⊕mi。因为ntz(x)表示x的二进制表示尾部0的个数,故假设当前加密块为n个,则使用到l0的次数为n/2,同时利用l0、l1…的关系进行SPA,重新组合它们之间的泄漏信息,获取更加精准的l0的值,具体的算法流程如下图7所示。

图7 使用SPA猜测l0的流程
总结
本文作者就“OCB中的所有操作都需要保护吗?如果需要,它们需要相同级别的保护吗?”的问题展开讨论,作者通过展示针对不同保护级别的OCB的几次攻击来回答这个问题。首先,作者表明,可以针对初始化函数和关联数据的处理进行最简单的DPA攻击。接下来,假设第一级保护可以防止上述提到的攻击,作者对用于生成密文块的加密块进行了攻击,可以使用两种方法,第一种是简单的将白化值作为掩码进行二阶DPA攻击,同时还提供了一种改进的(一阶)DPA攻击方法,以更高的(时间)密钥猜测复杂度为代价,降低了二阶攻击的数据复杂度。最后,作者考虑了这样一种情况,即所有的分组密码块都受到了强有力的保护。作者表明,使用SPA的方法可以得到白化值l0,该数值的恢复会对OCB3算法的完整性和机密性造成威胁。
参考资料
[1] Berti, F., S. Bhasin, J. Breier, X. Hou, R. Poussier, F.-X. Standaert, and B. Udvarhelyi. “A Finer-Grain Analysis of the Leakage (Non) Resilience of OCB”. IACR Transactions on Cryptographic Hardware and Embedded Systems, vol. 2022, no. 1, Nov. 2021, pp. 461-8, doi:10.46586/tches.v2022.i1.461-481.
