非入侵式攻击之交叉相关分析原理与实战

非入侵式攻击之交叉相关分析原理与实战

背景介绍

非入侵式攻击测试利用了隐藏在密码模块中或周围的物理量的有偏性，这种依赖于秘密信息的有偏量被称为泄露，测试泄露是否存在的测试即为泄露分析。简单能量分析（Simple Power Analysis，SPA）和差分能量分析（Differential Power Analysis，DPA）都是《GB/T 37092-2018 信息安全技术 密码模块安全要求》中规定的非入侵式攻击测试项。SPA需要直接（例如，通过视觉）分析密码模块在执行密码过程中各指令的能量消耗模式。通过监视密码模块能量消耗的变化，可以发现所执行密码算法的模式和实现方法，从而获取密钥值，文献^[1] 给出了一种Cross-Correlation方法，属于SPA的代表方法。

一阶DPA具有相同的目的，但是为了分析密码模块能量消耗的变化，使用了统计方法（例如，均值差、相关系数）对能量消耗进行统计分析，从而获取密钥值。文献^[2]中提出的方法也称为Cross-Correlation，但这是一种DPA类型的统计分析方法，它源自文献^[3]的碰撞相关攻击。本文主要讨论这种DPA型的Cross-Correlation。

Cross-Correlation分析^[2]，中文译为交叉相关分析。根据采集到的能量波形，可执行交叉相关分析来检索密码算法指令序列，进行DPA泄露检测。该功能可以获得波形中与密钥信息相关的敏感操作在何处执行的信息，其结果图也可以帮助测评人员识别针对侧信道分析的一些防护对策。

分析原理

在已知加密算法结构的条件下，对采集到的一组不同明文、相同密钥加密得到的若干条波形进行交叉相关分析时，设定两个指针沿横轴滑动，每滑动到一个地方，都计算一下两个指针所指的两列波形点之间的相关系数。当滑动位置遍历所有横坐标后，两个指针对应的相关系数可以形成一张二维的图，命名为交叉相关图。该实验图能够可视化对齐后的多条波形中不同横坐标受明文影响的关系，进而有助于帮助我们区分不同操作。在交叉相关图中，用亮点来表示相关性的强弱。色带上亮点明显的位置，相关性比较强，表示一个特定值在运行过程中的多次泄露，这与碰撞攻击是类似的。我们可以由此对敏感操作进行定位，进而通过识别这些操作来恢复出密钥。

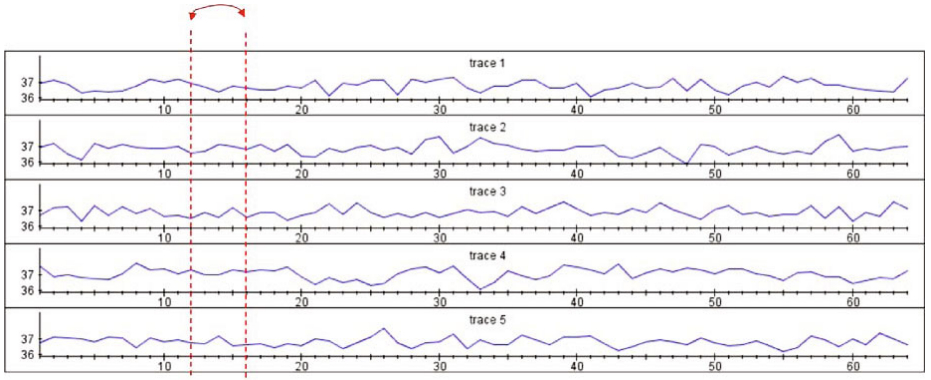
图片来源：文献[2]

功能说明

北京数缘科技有限公司自主研发的侧信道分析测评软件Detector集成了交叉相关分析，该功能的参数设置界面如图所示。

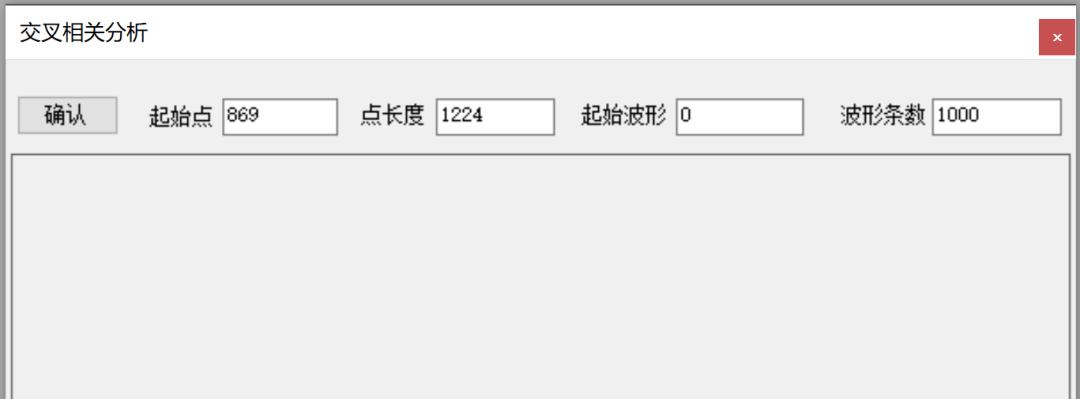
交叉相关分析控制面板

对话框中的文本框含义如下：

• 起始点、点长度：用于做交叉相关分析的起始采样点与长度，这部分的参数可以通过选中波形中的一部分进行自动填写。
• 起始波形：所选处理波形的起始编号。
• 波形条数：所选出来波形的总条数。

通过文本框确定待分析波形段后，点击“确认”执行交叉相关分析，在窗体下方生成计算出来的交叉相关图，图中绿色代表正相关，红色代表负相关，相关性性越强颜色越亮。消耗时间会通过日志进行显示。

案例实现

我们基于一款STM32F4系列单片机的开发板实现了无防护的RSA算法，采用数缘科技自主研发的多功能侧信道分析仪采集其能量波形。RSA算法的密钥信息主要落在平方和乘法的操作上，因而可以通过计算交叉相关系数，生成一张交叉相关图作为可视化结果，以达到定位不同运算操作、恢复密钥的目的。

多功能侧信道分析仪能量分析连线图

首先需要采集一组符合要求的RSA加密的波形。这里为了有明显直观的效果，采集了1000条波形。示例波形如下图所示。

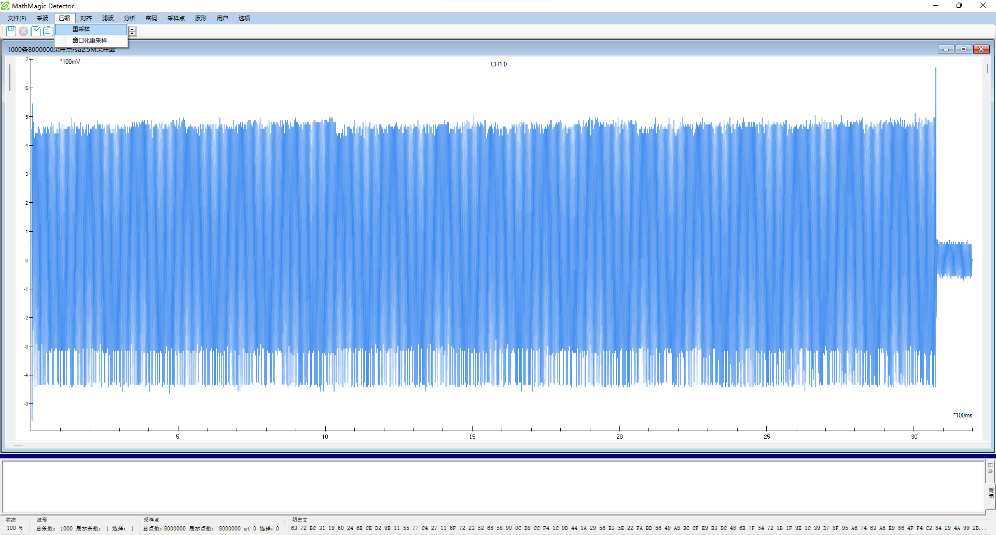
RSA示例波形

选中待分析的波形段，点击“确认”执行交叉相关分析，在窗体下方生成了计算得到的交叉相关图，如下图所示。取平方对应的Square操作简称为S操作，而乘法对应的Mulitiply操作简称为M操作，图中S、M操作都已标出。色带颜色较亮，且都是表示正相关关系的绿色，说明对应的是取平方的S操作；色带为红绿相间，且颜色较暗，说明对应的是乘法的M操作。一个S操作后紧跟一个M操作对应密钥1，而一个S操作后还是S操作，说明前一个S操作对应密钥0。由图可以识别出操作SMSSSMSSSMSSMSMSMSMSMSMSSMSMSSSSSM，对应密钥1001001011111101100001。

交叉相关图

适用场景

交叉相关分析的强大之处在于，它能够有效攻破RSA算法的多种防护对策。其一，是Multiply-Always，也就是添加伪操作。该措施具体执行时，逐比特扫描密钥，当密钥为0时，执行完取平方操作后再乘以底数（或随机数），但是将计算结果丢弃不用。也就是说，再扫描下一比特的密钥时，不使用乘以底数之后的值，而是使用取平方操作后、乘以底数之前的值，因此乘以底数这个伪操作并不影响加密结果，只是使扫描每一比特密钥时都有一个取平方操作和一个乘法操作。其二则是掩码，当模幂运算的底数或模数被随机掩码掩盖时，交叉相关分析仍然有效，因为它关心的是两处泄露的值是否总是相同，只要二者相同，哪怕被相同的随机掩码掩盖住，这种“相同泄露值”的情况仍然能被发现。

交叉相关分析可适用于添加防护对策的RSA算法加密。以两种泄露情况为例：

第一种情况：这种情况下交叉相关分析利用的是：真正的乘法操作因为都需要调用明文而产生了相关性。如果是正常的乘法操作，同一条波上的多个乘法操作都需要调用到相同的明文，这些乘法操作之间具有相关性；而乘以一个随机数的伪操作没有调用明文，因此不具有相关性。以此可以区分哪些乘法操作是模幂运算的一部分，而哪些乘法操作只是伪操作。

如下图所示，首先，同一操作之间的较强的相关关系，在图中以白色方块表示；对于正常的乘法操作，也就是图中白色的M操作，都需要调用到相同的明文，它们之间存在相关性，在图中以橘色的方块表示。若当前操作为伪操作，在图中以红色的M操作表示，乘数是一个随机数而不是明文，那么该操作与正常的乘法操作之间不具有相关性，在图中仍是黑色的方块。

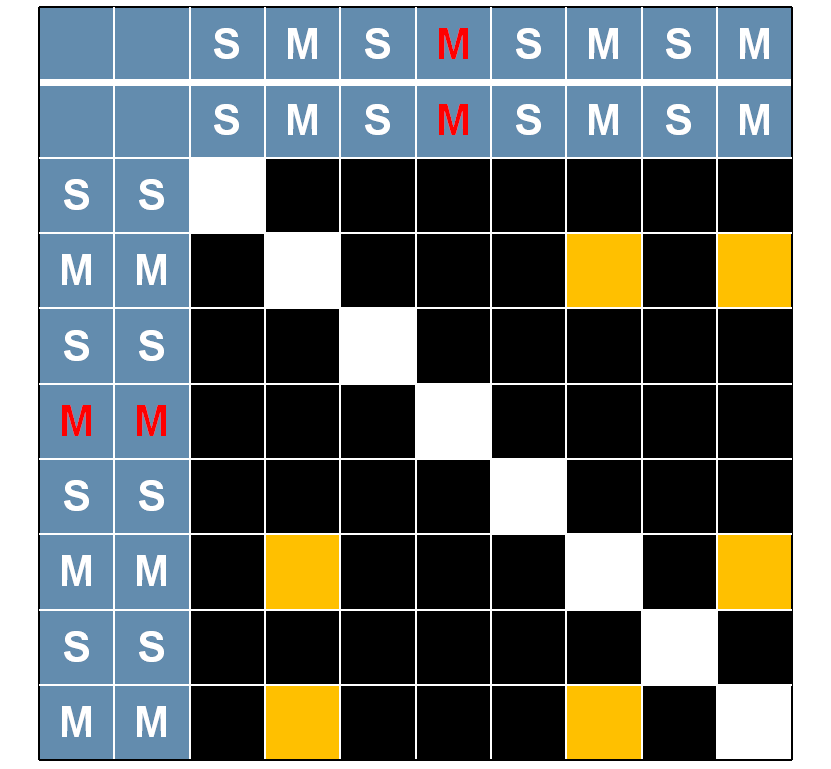
第一种情况交叉相关图

第二种情况：这种情况下交叉相关分析利用的是：前一个操作的输出结果可能是后一个操作的输入内容。如果是正常的操作，那么前一个操作的输出结果就是后一个操作的输入内容，前一个操作与后一个操作之间因为调用了同一个值，会产生相关性；如果当前的乘法操作为伪操作，乘以一个随机数之后就将该计算结果丢弃，那么下一操作的输入并不是该操作的输出，而是上一操作的输出，所以下一个操作会与上一个操作之间，也就是与伪操作相邻的两个取平方操作之间具有相关性。

如图所示，同样地，同一操作之间的较强的相关关系，在图中以白色方块表示；对于正常的操作，也就是图中白色的S、M操作，后一个操作的输入是前一个操作的输出，故前后两个相邻的操作之间存在相关性，在图中以黄色的方块表示。若是当前操作为伪操作，在图中以红色的M操作表示，乘以一个随机数之后就将该计算结果丢弃，那么与伪操作相邻的两个取平方操作之间具有相关性，在图中以橘色方块表示。

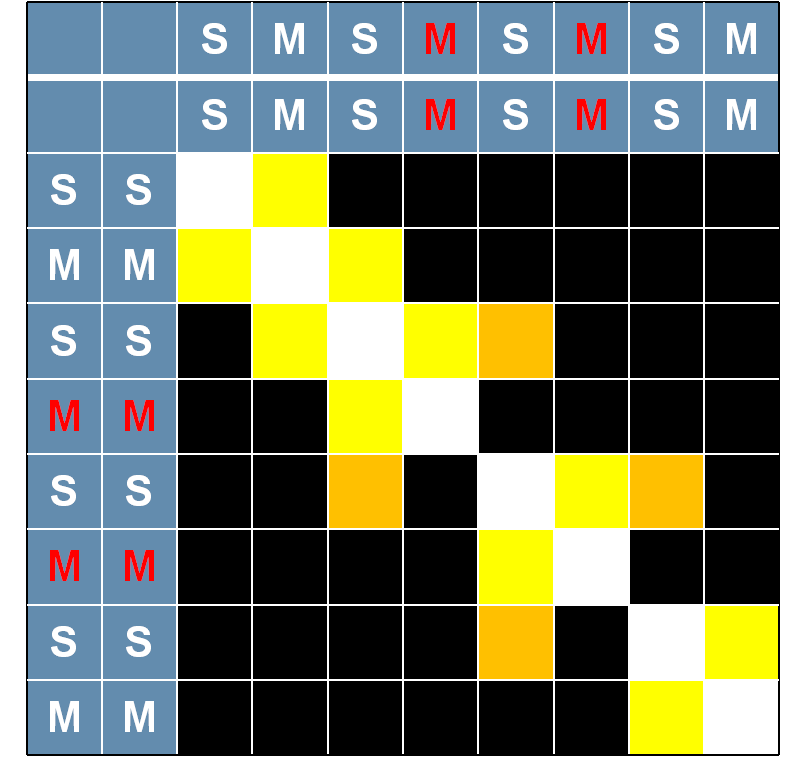
第二种情况交叉相关图

参考资料

[1] Thomas S. Messerges, Ezzy A. Dabbish, Robert H. Sloan. Power Analysis Attacks of Modular Exponentiation in Smartcards. CHES 1999, LNCS 1717, pp. 144−157, 1999.

[2] Marc F. Witteman, Jasper G.J. van Woudenberg, Federico Menarini. Defeating RSA Multiply-Always and Message Blinding Countermeasures. CT-RSA 2011, LNCS 6558, pp. 77-88, 2011.

[3] Christophe Clavier, Benoit Feix, Georges Gagnerot, Myl`ene Roussellet, and Vincent Verneuil. Improved Collision-Correlation Power Analysis on First Order Protected AES. CHES 2011, LNCS 6917, pp. 49-62, 2011.